Hamiltoniano para semimetales de Weyl tipo I – Grushin #
En el presente informe se presentan los resultados de la caraterización teorica de los semimetales de Weyl (WSM, por sus siglas en inglés). Los electrones en dichos semimetales se describen de forma efectiva por la ecuación de Weyl y, en consecuencia, tienen una relación de dispersión lineal característica de las partículas relativistas sin masa. Los WSM se caracterizan por tener un gap que se cierra en una serie de puntos protegidos por las simetrías del cristal, llamados nodos de Weyl. Dependiendo si el sistema rompe o no la simetría de Lorentz, los WSM pueden ser de tipo I, tipo II y en recientes descubrimientos se reportan los tipo III; sin embargo, los de mayor atención en este trabajo serán los primeros dos, por ser los más estudiados tanto teórica como experimentalmente, lo cual, eventualmente, permitirá comparar los resultados obtenidos. Una particularidad más de los WSM que permitirá ampliar su estudio es la cuasipartícula que lo caracteriza, el fermión de Weyl. Cuando dichos fermiones experimentan variaciones del espacio-tiempo obedecen leyes simples que pueden expresarse en términos de pseudocampos electromagnéticos, y es probable que la aparición de este fenómeno modifique la estructura de bandas, la densidad de estados y con ello la conductividad del material, por lo que en este trabajo se realizará la descripción teórica de los WSM cuando son perturbados periódicamente de manera mecánica.
Note
El objetivo general de este notebook es explorar el Hamiltoniano presentado en el Review[1]
Los conceptos a introducir serán:
Hamiltoniano para un semimetal del Weyl Tipo I
Relación de dispersión generada por este tipo de materiales
Fuente: R. Ilan, A. G. Grushin, and D. I. Pikulin, Pseudo-electromagnetic fields in 3d topological semimetals,Nature Reviews Physics2, 29 (2020).
Hamiltoniano del sistema #
Expresión de la forma exponencial#
Acerca de la notación:
\(t_\parallel\): es el parametro que da el hooping en el mismo plano de la celda unitaria.
\(t_\perp\): es el parametro que da el hooping fuera del plano de la celda unitaria.
\(m\): es la distancia en el espacio reciproco por la que estarán desplazados respecto al 0
Show code cell source
from pylab import *
import multiprocessing as mp
mpl.rcParams.update({'font.size': 22, 'text.usetex': True})
mpl.rcParams.update({'axes.linewidth':1.5})
mpl.rcParams.update({'axes.labelsize':'large'})
mpl.rcParams.update({'xtick.major.size':12})
mpl.rcParams.update({'xtick.minor.size':6})
mpl.rcParams.update({'ytick.major.size':12})
mpl.rcParams.update({'ytick.minor.size':6})
mpl.rcParams.update({'xtick.major.width':1.5})
mpl.rcParams.update({'xtick.minor.width':1.0})
mpl.rcParams.update({'ytick.major.width':1.5})
mpl.rcParams.update({'ytick.minor.width':1.0})
Multiprocesing#
Multiprocessing permite agilizar la forma en la que se calculan los eigenestados generando una red de valores mapeados
Show code cell source
import multiprocessing as mp
from pylab import *
import plotly.graph_objects as go
from plotly import *
Show code cell source
res=pi/101 #resolucion
# fig = plt.figure()
# ax= fig.add_subplot(projection='3d')
# x= k_xb
# z= k_zb
# X, Z = meshgrid(x,z)
# ax.scatter(X,Z,Enm ) #s de size y c de color
k_xb,k_yb,k_zb=arange(-pi,pi,res),arange(-pi,pi,res),arange(-pi,pi,res)
a = 0.8
m = 0
tp = 0.1
tl = tp*sqrt(1-m**2)
def HWeyl(k_x,k_y,k_z):
""""Esta función permite generalizar al hamiltoniano en todo el espacio reciproco"""
HW = array([[tp*(cos(k_z*a)-m), tl*sin(k_x*a)-1J*tl*sin(k_y*a)],
[tl*sin(k_x*a)+1J*tl*sin(k_y*a), -tp*(cos(k_z*a)-m)]])
return HW
Show code cell source
def EigenV(k):
""""Esta función permite recopilar toda la información de kx, ky, kz, en una sola variable, además,
recoge toda la información de de los eigenvalores de energía E"""
k_x,k_y,k_z=k
E=eigvalsh(HWeyl(k_x,k_y,k_z))
return E
Show code cell source
"""A continuación, se presenta el mayado del espacio reciproco y su incorparacion en una variable generalizada, k.
La cual permite generar una matriz"""
a_d= len(k_xb) #dimension del arreglo
KX,KZ = meshgrid(k_xb,k_zb)
KX = KX.reshape((a_d*a_d,))
KZ = KZ.reshape((a_d*a_d,))
k = column_stack((KX,zeros_like(KX),KZ))
Show code cell source
%%time
""" Aquí se extrae la información aplicando la funcion EigenV al column stack de k, unas obtenidos os eigenvalores Ek
se arreglan en una lista y luego en un arrelo que permita su graficación"""
Ek = map(EigenV,k) #función y los valores que toma
Ek = array(list(Ek))
print(Ek)
[[-0.1 0.1 ]
[-0.10118535 0.10118535]
[-0.10237278 0.10237278]
...
[-0.10240146 0.10240146]
[-0.10120134 0.10120134]
[-0.1 0.1 ]]
CPU times: user 1.84 s, sys: 0 ns, total: 1.84 s
Wall time: 1.84 s
Show code cell source
"""Se toman los Ek positivos en una lista Enm y los negativos en otra, pero para ello se deben de transponer
pues estan como columnas y se necesitan en formas de filas"""
Enm = Ek.T[0].reshape((a_d,a_d))#primer parentesis d ela funcion, segundos de la tupla
Enp = Ek.T[1].reshape((a_d,a_d))
KX,KZ = meshgrid(k_xb,k_zb)
# plot(KX,Enp)
# plot(KX,Enm)
Show code cell source
DATA = [ go.Surface( z=Enm, x=(KX),y=(KZ),opacity=0.9, colorbar_x=0.75,colorscale='deep'),
go.Surface( z=Enp,x=KX,y=KZ,opacity=0.6, colorbar_x=0.9,showscale=False)]
#
Show code cell source
fig=go.Figure(data=DATA)
fig.update_layout( autosize=False,
width = 800, height = 500,
margin= dict(l=80, r=80, b=65, t=90),
scene = dict(xaxis_title="kx",
yaxis_title="ky",
zaxis_title="E [t]",
xaxis = dict(showbackground=False),
yaxis = dict(showbackground=False),
zaxis = dict(showbackground=False)))
fig.show()
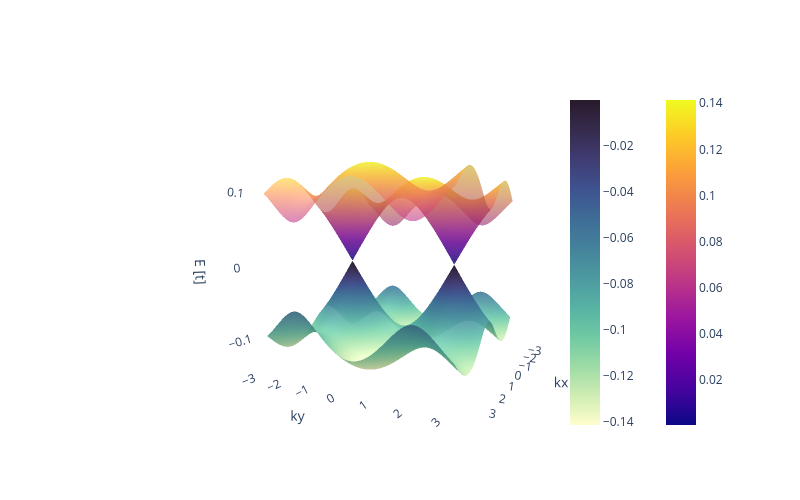
En esta figura se presenta una realcion de dispersion propia de un semimetal de Weyl tipo I. Dicha relacion se caracteriza porque la banda de conducción y valencia son simetricas al plano \(K_x, K_y\)