Hamiltoniano para semimetales de Weyl Type II–Minimal Models
#

El objetivo general de este notebook es explorar el Hamiltoniano presentado en el artículo [1]

Los conceptos a introducir serán:

  • Hamiltoniano para un semimetal del Weyl

  • Relación de dispersión generada por este tipo de materiales

A diferencia del hamiltoniano explorado anteriormente, este econtiene un parametro \gamma, que permite estudiar la transición de fase de un semimetal de Weyl tipo I a uno tipo II. Adicionalmente, este notebook se enfocara sólo en la fase correspondiente al semimemtal de Weyl tipo II (\(\gamma\) = 3t)..

Fuente: T. M. McCormick, I. Kimchi, and N. Trivedi. Minimal Models for Topological Weyl Semimetals.Phys. Rev. B, 95(7):075133, Feb 2017

\[\begin{eqnarray*} H(k) = \left[ \begin{array}{cc} \gamma (cos(k_xa)-cos(k_0a))-2t(sin(k_za) ) & -m(2-cos(k_ya)-cos(k_za))+2t_x(cos(k_xa)-cos(k_0a))+2it(sin(k_ya))\\-m(2-cos(k_ya)-cos(k_za))+2t_x(cos(k_xa)- cos(k_0a))-2it(sin(k_ya))& \gamma (cos(k_xa) -cos(k_0a))+2t(sin(k_za)) \end{array} \right] \end{eqnarray*}\]

En su forma exponencial:

(3)#\[\begin{eqnarray} H(k) = \left[ \begin{array}{cc} \frac{\gamma }{2}(e^{ik_xa}+e^{-ik_xa}-e^{ik_0a}-e^{-ik_0a})-\frac{t}{i}(e^{ik_za}-e^{-ik_za}) & -\frac{m}{2}(4-e^{ik_ya}-e^{-ik_ya}-e^{ik_za}-e^{-ik_za})+t_x(e^{ik_xa}+e^{-ik_xa}-e^{ik_0a}-e^{-ik_0a})+t(e^{ik_ya}-e^{-ik_ya})\\ -\frac{m}{2}(4-e^{ik_ya}-e^{-ik_ya}-e^{ik_za}-e^{-ik_za})+t_x(e^{ik_x}+e^{-ik_xa}-e^{ik_0a}-e^{-ik_0a})-t(e^{ik_ya}-e^{-ik_ya})& \frac{\gamma }{2}(e^{ik_xa}+e^{-ik_xa}-e^{ik_0a}-e^{-ik_0a})+\frac{t}{i}(e^{ik_za}-e^{-ik_za}) \end{array} \right] \end{eqnarray}\]

Multiprocesing#

Hide code cell source 
from pylab import *
import multiprocessing as mp
Hide code cell source 
def EigenV(k):
    k_x,k_y,k_z=k
    E=eigvalsh(HWeyl(k_x,k_y,k_z))
    return E
Hide code cell source 
res=pi/101 #resolucion

k_xb,k_yb,k_zb=arange(-pi,pi,res),arange(-pi,pi,res),arange(-pi,pi,res)

a  = 1
k_0= pi/2
   #Weyl positions
tx = 0.5      
t  = 0.5
m  = 2*t
γ  = 3*t
def HWeyl(k_x,k_y,k_z):   
    HW = array([[γ*(cos(k_x)-cos(k_0))-2*t*sin(k_z),   -(m*(2-cos(k_y)-cos(k_z))+2*tx*(cos(k_x)-cos(k_0)))+2J*t*sin(k_y)],
                [ -(m*(2-cos(k_y)-cos(k_z))+2*tx*(cos(k_x)-cos(k_0)))-2J*t*sin(k_y), γ*(cos(k_x)-cos(k_0))+2*t*sin(k_z)]])
    return HW
Hide code cell source 
a_d= len(k_xb) #dimension del arreglo
KX,KZ = meshgrid(k_xb,k_zb)
KX    = KX.reshape((a_d*a_d,))
KZ    = KZ.reshape((a_d*a_d,))

k     = column_stack((KX,zeros_like(KX),KZ))
Hide code cell source 
%%time 

Ek = map(EigenV,k) #función  y los valores que toma
Ek = array(list(Ek))
print(Ek)

[[-2.5        -0.5       ]
 [-2.49975814 -0.49879071]
 [-2.4990328  -0.49516399]
 ...
 [-2.49782258 -0.48912547]
 [-2.49903186 -0.49516493]
 [-2.49975791 -0.49879094]]
CPU times: user 2.43 s, sys: 39 ms, total: 2.47 s
Wall time: 2.46 s
Hide code cell source 
Enm = Ek.T[0].reshape((a_d,a_d)).T#primer T para +/- segundo para X->Z
Enp = Ek.T[1].reshape((a_d,a_d)).T


KX,KZ = meshgrid(k_xb,k_zb)
Hide code cell source 
import plotly.graph_objects as go
Hide code cell source 
DATA = [ go.Surface( z=Enm, x=(KX),y=(KZ),opacity=0.9,  colorbar_x=0.75,colorscale='deep'),
        go.Surface( z=Enp,x=KX,y=KZ,opacity=0.6, colorbar_x=0.9)]
Hide code cell source 
fig = go.Figure( data=DATA )

fig.update_layout( autosize=False,
                   width = 800, height = 500,
                   margin= dict(l=65, r=50, b=65, t=90),
                   scene = dict(xaxis_title="kx", 
                                yaxis_title="ky", 
                                zaxis_title="E [t]", 
                                xaxis = dict(showbackground=False), 
                                yaxis = dict(showbackground=False),
                                zaxis = dict(showbackground=False)))

fig.show()

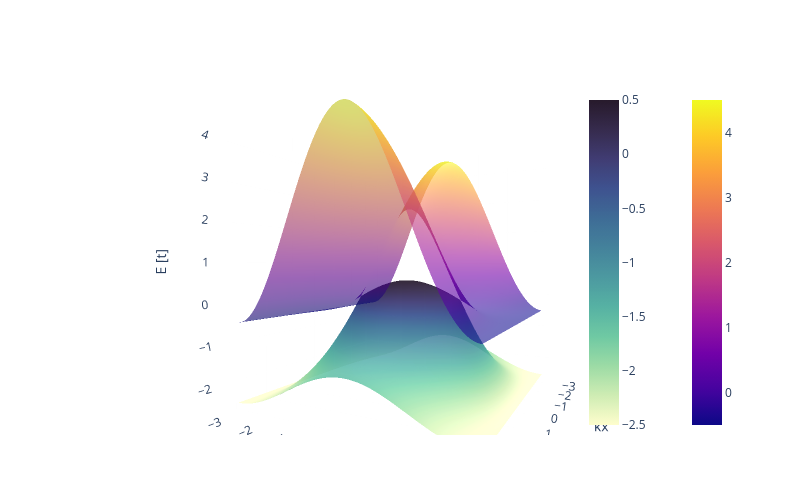
En esta figura se presenta una realcion de dispersion propia de un semimetal de Weyl tipo II. Dicha relación se caracteriza porque la banda de conducción y valencia NO son simetricas al plano \(K_x, K_y\). Es decir, se observa que los conos (conos de Dirac) se encuentran inclinados respecto al eje \(E[t]\)

Semimetal de Weyl Tipo II