Hamiltoniano del sistema – Minimal Models #
Show code cell source
from pythtb import *
from pylab import *
Show code cell source
import glob
from matplotlib.ticker import (MultipleLocator,
FormatStrFormatter,
AutoMinorLocator)
mpl.rcParams.update({'font.size': 22, 'text.usetex': True})
mpl.rcParams.update({'axes.linewidth':1.5})
mpl.rcParams.update({'axes.labelsize':'large'})
mpl.rcParams.update({'xtick.major.size':12})
mpl.rcParams.update({'xtick.minor.size':6})
mpl.rcParams.update({'ytick.major.size':12})
mpl.rcParams.update({'ytick.minor.size':6})
mpl.rcParams.update({'xtick.major.width':1.5})
mpl.rcParams.update({'xtick.minor.width':1.0})
mpl.rcParams.update({'ytick.major.width':1.5})
mpl.rcParams.update({'ytick.minor.width':1.0})
Show code cell source
from palettable.cubehelix import Cubehelix
palette = Cubehelix.make(start=-0.5, rotation=0.3,reverse=True,n=10)
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[3], line 1
----> 1 from palettable.cubehelix import Cubehelix
2 palette = Cubehelix.make(start=-0.5, rotation=0.3,reverse=True,n=10)
ModuleNotFoundError: No module named 'palettable'
Show code cell source
#Parámetros
a = 1.0
k_0= pi/2
tx = 1
t = 1
m = 2*t
γ = 0
A_x= 0.0
A_y= +0.0
A_z= 0.0
##################----------------Inicia TB----------------##################
lat= [[a,0,0],[0,a,0],[0,0,a]]
orb= [[0,0,0],[1/2,1/2,1/2]] #H, solo los sitios A[000] B1/2[111]
WSH = tb_model(3,3,lat,orb)
#DIAGONAL
#γ*(cos(k_x)-cos(k_0))-2*t*sin(k_z)
# γ[coskx]
WSH.set_hop(γ/2, 0, 0,[1,0,0])#de que sitio a que sitio va el hoping, [la exp que lleva ese parametro], Conjugado ya no es
# -2tsinkz #necesario, está implícito porque es Hermitiano.
WSH.set_hop(-t/1J, 0, 0,[0,0,1])
#Hermitiano [1,1]
WSH.set_hop(γ/2, 1, 1,[1,0,0])
WSH.set_hop(t/1J, 1, 1,[0,0,1])
WSH.set_onsite([-γ*cos(k_0)+A_z,-γ*cos(k_0)-A_z]) # No hay hooping, es energia
#FUERA DE LA DIAGONAL
# -[m*(2-cos(k_y)-cos(k_z))+2*tx*(cos(k_x)-cos(k_0))]+2J*t*sin(k_y)
# 2txcosk_0
WSH.set_hop(-2*m+2*(tx)*cos(k_0)+A_x, 0, 1,[0,0,0])
#mcosky+ 2itsin(ky)
WSH.set_hop(m/2+t, 0, 1,[0,1,0])
WSH.set_hop(m/2-t, 0, 1,[0,-1,0])
# mcoskz
WSH.set_hop(m/2, 0, 1,[0,0,1])
WSH.set_hop(m/2, 0, 1,[0,0,-1])
# tx(coskx)
WSH.set_hop(-tx+A_x, 0, 1,[1,0,0])
WSH.set_hop(-tx+A_x, 0, 1,[-1,0,0])
###############---------Inicia extraccion de información-----------##############
k=[[-0.5,0,0],[0,0,0.0],[0.5,0,0]] # Punto por los cuales que quiero que pase. Son los punto de al simetria
#unidades en unidades de V de red 1=2pi/a
# k=[[0,-0.5,0],[0,0,0.0],[0.,0.5,0] ]
# k=[[0,0,-0.5],[0,0,0.0],[0.,0.,0.5]]
k_label=[r"$-X$",r"$\Gamma$",r"$X$"]
(k_vec,k_dist,k_node)=WSH.k_path(k,1001,report=False)
Ek,ψ =WSH.solve_all(k_vec,eig_vectors=True)
#######################---Graficos----######################
fig,ax = plt.subplots(ncols=2,nrows=1,figsize=(18,6),
gridspec_kw = {'wspace':0.4, 'hspace':0, 'width_ratios': [1, 1]})
ax[0].plot(k_dist,Ek[0,:],zorder=1,lw=1.5)
ax[0].plot(k_dist,Ek[1,:],zorder=1,lw=1.5)
ax[0].set_xticks(k_node) # puntos de alta simetria, valor que correspomde en k_path
ax[0].set_xticklabels(k_label )
ax[0].set_yticks([-4,-2,0.,2,4])
# xsticklabels(k_label)
ax[0].spines['right'].set_visible(False)
ax[0].spines['top'].set_visible(False)
ax[0].set_ylabel(r"$E[t]$",fontsize=26)
ax[0].set_xlabel(r"$K_x$",fontsize=26)
k=[[-0.5,0,0],[0,0,0.0],[0.5,0,0]]# Punto por los cuales que quiero que pase. Son los punto de al simetria
#unidades en unidades de V de red 1=2pi/a
(k_vec,k_dist,k_node)=WSH.k_path(k,1001,report=False)
Ek,U=WSH.solve_all(k_vec,eig_vectors=True)
ax[1].plot(k_dist,Ek[0,:],zorder=1,lw=1.5)
ax[1].plot(k_dist,Ek[1,:],zorder=1,lw=1.5)
# puntos de alta simetria, valor que correspomde en k_path
ax[1].set_yticks([-0.2,0.,0.2])
ax[1].set_ylim([-0.2,0.2])
ax[1].set_xlim([0.1,0.9])
# xsticklabels(k_label)
ax[1].spines['right'].set_visible(False)
ax[1].spines['top'].set_visible(False)
ax[1].set_ylabel(r"$E[t]$",fontsize=26)
ax[1].set_xlabel(r"$K_x$",fontsize=26)
savefig("WSMMMBulkGapTI.pdf",bbox_inches='tight')
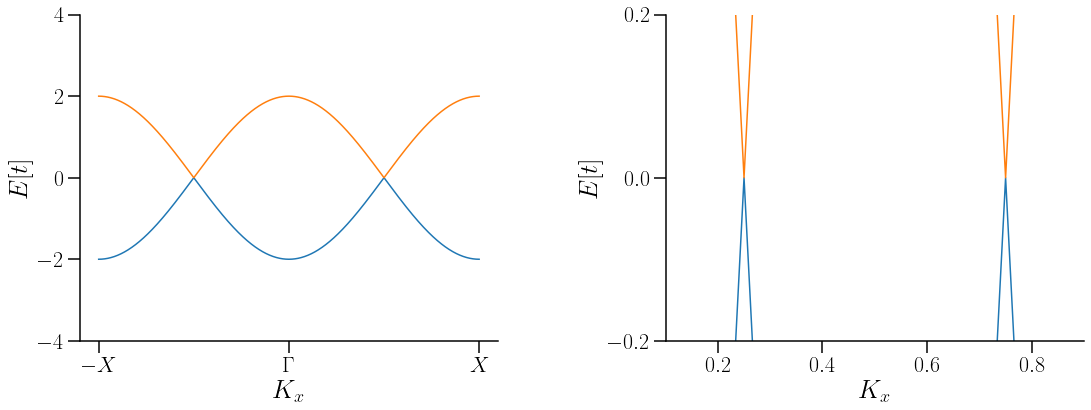
Show code cell source
L= 100
NY_WSM=WSH.cut_piece(L,1,glue_edgs=False)
NX_WSM=WSH.cut_piece(L,0,glue_edgs=False)
NZ_WSM=WSH.cut_piece(L,2,glue_edgs=False)
Exploración de la estructura de bandas en distintos planos del material#
Show code cell source
k=[[0,0],[0.5,0],[1.0,0]]
k_label1=[r"$\Gamma$",r"$Y$",r"$\Gamma$"]
(k_vec,k_dist,k_node)=NX_WSM.k_path(k,501, report=False)
EkfinX10=NX_WSM.solve_all(k_vec)
k=[[0,0],[0,0.5],[0,1.0]]
k_label2=[r"$\Gamma$",r"$Z$",r"$\Gamma$"]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,501, report=False)
EkfinY10=NY_WSM.solve_all(k_vec)
k=[[0,0],[0.5,0],[1.0,0]]
k_label3=[r"$\Gamma$",r"$X$",r"$\Gamma$"]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,501, report=False)
EkfinZ10=NZ_WSM.solve_all(k_vec)
Show code cell source
fig,ax = plt.subplots(ncols=3,nrows=1,figsize=(20,6),
gridspec_kw = {'wspace':0.2, 'hspace':0, 'width_ratios': [1, 1,1]})
for n in range(0, len(EkfinX10)):
ax[0].plot(k_dist,EkfinX10[n,:], c='black', alpha=0.6,linewidth=1.1) #la long de Ek fin tiene todo
ax[1].plot(k_dist,EkfinY10[n,:], c='black', alpha=0.6,linewidth=1.1) #la long de Ek fin tiene todo
ax[2].plot(k_dist,EkfinZ10[n,:], c='black', alpha=0.6,linewidth=1.1) #la long de Ek fin tiene todo
for i in range(0,3):
ax[i].set_xticks(k_node) # puntos de alta simetria, valor que correspomde en k_path
# ax[i].set_yticks([-2,0.,2])
# xsticklabels(k_label)
ax[i].spines['right'].set_visible(False)
ax[i].spines['top'].set_visible(False)
ax[0].set_xticklabels(k_label1 )
ax[1].set_xticklabels(k_label2 )
ax[2].set_xticklabels(k_label3 )
ax[0].set_ylabel(r"$E[t]$",fontsize=26)
ax[0].set_xlabel(r"Finite System in $X|_{K_Z=0}$",fontsize=26)
ax[1].set_xlabel(r"Finite System in $Y|_{K_X=0}$",fontsize=26)
ax[2].set_xlabel(r"Finite System in $Z|_{K_Y=0}$",fontsize=26)
# puntos de alta simetria, valor que correspomde en k_path
savefig("Finite_systems_MM_TII.pdf",bbox_inches='tight')

A diferencia de los hamiltonianos anteriores, en la estructura de bandas de este se pude observar una line aque une a los dos nodos de Weyl. Dicha línea recibe el nombre de Arco de Fermi.
Exploración de la estructura de bandas en el material finito en X#
Show code cell source
###-------Finito en X-------#
z=0
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NX_WSM.k_path(k,101, report=False)
EkfinX10=NX_WSM.solve_all(k_vec)
z=0.1
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinX11=NX_WSM.solve_all(k_vec)
z=0.2
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinX12=NX_WSM.solve_all(k_vec)
z=0.3
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinX13=NX_WSM.solve_all(k_vec)
z=0.4
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinX14=NX_WSM.solve_all(k_vec)
z=0.5
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinX15=NX_WSM.solve_all(k_vec)
Show code cell source
fig,ax=plt.subplots(ncols=3,nrows=2,figsize=(20,12),
gridspec_kw = {'wspace':0.2, 'hspace':0.4, 'width_ratios': [1,1,1]})
for n in range(0, len(EkfinX10)):
ax[0,0].plot(k_dist,EkfinX10[n,:], c='black', alpha=0.6) #la long de Ek fin tiene todo
ax[0,1].plot(k_dist,EkfinX11[n,:], c='black', alpha=0.6)
ax[0,2].plot(k_dist,EkfinX12[n,:], c='black', alpha=0.6)#la long de Ek fin tiene todo
ax[1,0].plot(k_dist,EkfinX13[n,:], c='black', alpha=0.6)
ax[1,1].plot(k_dist,EkfinX14[n,:], c='black', alpha=0.6)
ax[1,2].plot(k_dist,EkfinX15[n,:], c='black', alpha=0.6)
for i in range(0,2):
for j in range(0,3):
ax[i,j].spines['right'].set_visible(False)
ax[i,j].spines['top'].set_visible(False)
ax[0,0].set_ylabel(r"$E[t]$",fontsize=26)
ax[1,0].set_ylabel(r"$E[t]$",fontsize=26)
ax[0,0].set_xlabel(r"Finite systemy in $X|_{k_z=0.0}$",fontsize=26)
ax[0,1].set_xlabel(r"Finite system in $X|_{k_x=0.1}$",fontsize=26)
ax[0,2].set_xlabel(r"Finite systemy in $X|_{k_z=0.2}$",fontsize=26)
ax[1,0].set_xlabel(r"Finite system in $X|_{k_x=0.3}$",fontsize=26)
ax[1,1].set_xlabel(r"Finite systemy in $X|_{k_z=0.4}$",fontsize=26)
ax[1,2].set_xlabel(r"Finite system in $X|_{k_x=0.5}$",fontsize=26)
Text(0.5, 0, 'Finite system in $X|_{k_x=0.5}$')

Como se puede denotar en la figura anterior, la variación de \(k_z\) sila como evolucuiona la relacion de dispersion a lo alrgo de la primera mitad de la zona de Brillouin.
Show code cell source
fig=plt.figure(figsize=(12,6))
ax=fig.add_subplot(projection="3d")
# make the panes transparent
ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
# make the grid lines transparent
ax.xaxis._axinfo["grid"]['color'] = (1,1,1,0)
ax.yaxis._axinfo["grid"]['color'] = (1,1,1,0)
ax.zaxis._axinfo["grid"]['color'] = (1,1,1,0)
x=k_dist
x=k_dist
y=k_dist
y1=zeros(len(k_dist))
y2=zeros(len(k_dist))+0.25
x2=k_dist*10-2.5
X, Y=meshgrid(x,y)
for n in range(len(EkfinX10)):
ax.plot(x,y1, EkfinX10[n,:], c="black", alpha=0.6,linewidth=0.4)
ax.plot(x,y1+0.1, EkfinX11[n,:], c="black", alpha=0.2, linewidth=0.4)
ax.plot(x,y1+0.2, EkfinX12[n,:], c="black", alpha=0.3, linewidth=0.4)
ax.plot(x,y1+0.3, EkfinX13[n,:], c="black", alpha=0.3, linewidth=0.4)
ax.plot(x,y1+0.4, EkfinX14[n,:], c="black", alpha=0.3, linewidth=0.4)
ax.plot(x,y1+0.5, EkfinX15[n,:], c="black", alpha=0.3, linewidth=0.4)
# ax.plot(y1+1,x, EkfinY2[n,:], c="red", alpha=0.5)
# ax.plot(x,EkfinZ[n,:],y1, c="black", alpha=0.5)
ax.set_xlabel("$K_y$")
ax.set_ylabel("$K_z$")
ax.set_zlabel("E[t]")
ax.set_yticks([])
ax.set_zticks([-8,-5,-3,0,5,10, 13])
plt.tight_layout()
ax.view_init(0, -90)
savefig("Planes_Y_TII.pdf")
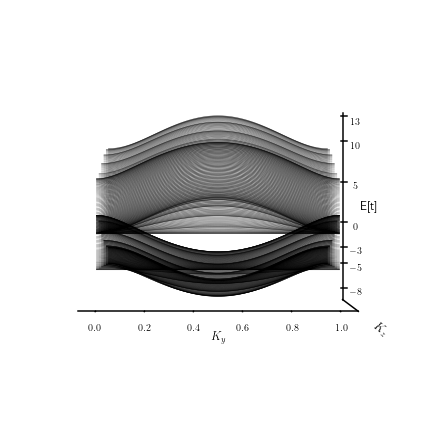
Exploración de la estructura de bandas en el material finito en Y#
Show code cell source
###-------Finito en Y-------#
z=0.
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY10=NY_WSM.solve_all(k_vec)
z=0.025
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY11=NY_WSM.solve_all(k_vec)
z=0.1
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY12=NY_WSM.solve_all(k_vec)
z=0.25
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY13=NY_WSM.solve_all(k_vec)
z=0.4
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY14=NY_WSM.solve_all(k_vec)
z=0.5
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY15=NY_WSM.solve_all(k_vec)
Show code cell source
fig,ax = plt.subplots(ncols=3,nrows=2,figsize=(20,12),
gridspec_kw = {'wspace':0.2, 'hspace':0.4, 'width_ratios': [1,1,1]})
for n in range(0, len(EkfinY10)):
ax[0,0].plot(k_dist,EkfinY10[n,:], c='black', alpha=0.6,linewidth=1.1) #la long de Ek fin tiene todo
ax[0,1].plot(k_dist,EkfinY11[n,:], c='black', alpha=0.6,linewidth=1.1)
ax[0,2].plot(k_dist,EkfinY12[n,:], c='black', alpha=0.6,linewidth=1.1)#la long de Ek fin tiene todo
ax[1,0].plot(k_dist,EkfinY13[n,:], c='black', alpha=0.6,linewidth=1.1)
ax[1,1].plot(k_dist,EkfinY14[n,:], c='black', alpha=0.6,linewidth=1.1 )
ax[1,2].plot(k_dist,EkfinY15[n,:], c='black', alpha=0.6,linewidth=1.1)
for i in range(0,2):
for j in range(0,3):
ax[i,j].spines['right'].set_visible(False)
ax[i,j].spines['top'].set_visible(False)
ax[0,0].set_ylabel(r"$E[t]$",fontsize=26)
ax[1,0].set_ylabel(r"$E[t]$",fontsize=26)
ax[0,0].set_xlabel(r"Finite system in $Y|_{k_z=0.0}$",fontsize=26)
ax[0,1].set_xlabel(r"Finite system in $Y|_{k_z=0.025}$",fontsize=26)
ax[0,2].set_xlabel(r"Finite system in $Y|_{k_z=0.10}$",fontsize=26)
ax[1,0].set_xlabel(r"Finite system in $Y|_{k_z=0.25}$",fontsize=26)
ax[1,1].set_xlabel(r"Finite system in $Y|_{k_z=0.40}$",fontsize=26)
ax[1,2].set_xlabel(r"Finite system in $Y|_{k_z=0.50}$",fontsize=26)
savefig("Perfil_Capas_WSM_TII.pdf", bbox_inches="tight")
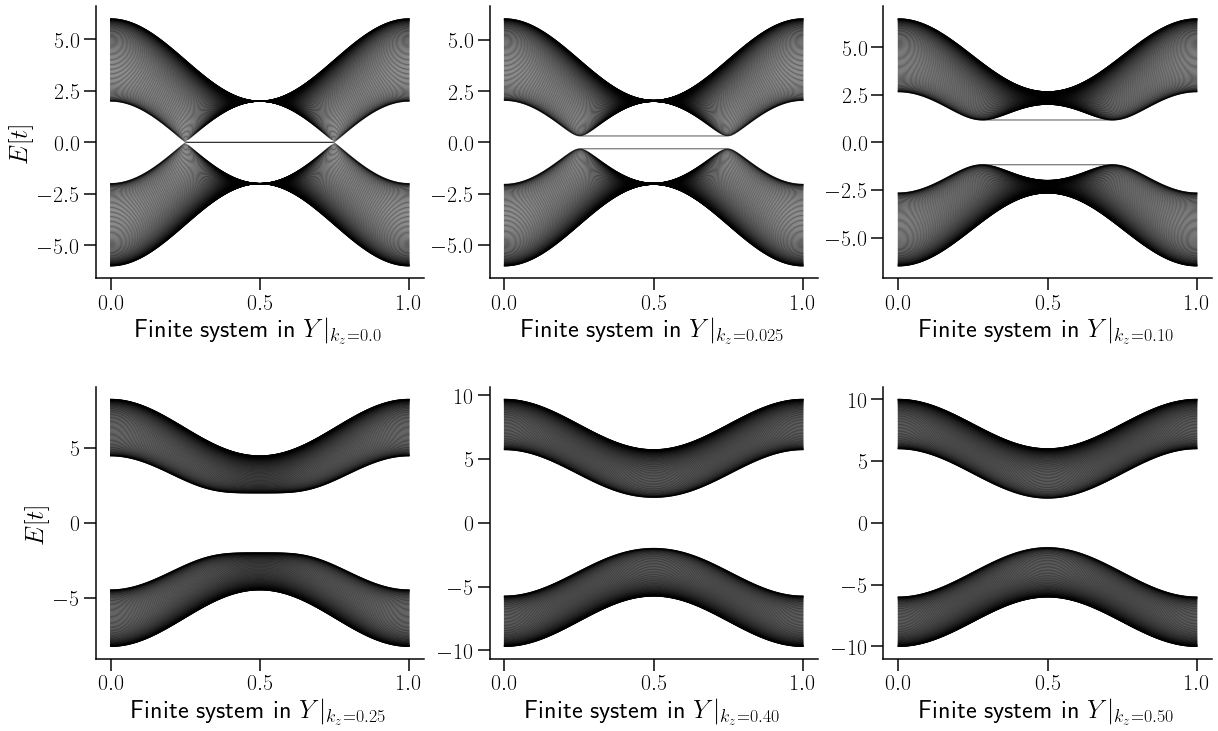
Se denota cómo los arcos de Fermi van evolucionando conforme se avanza en la zona de Brillouin. Si este avabce se hiciera continuo se formarian dos planos interceptados extactamente en el arco de Fermi. Dichos planos corresponderian a la superficie de Fermi.
Show code cell source
###-------Finito en Y-------#
z=0.
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY10=NY_WSM.solve_all(k_vec)
z=0.1
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY11=NY_WSM.solve_all(k_vec)
z=0.2
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY12=NY_WSM.solve_all(k_vec)
z=0.3
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY13=NY_WSM.solve_all(k_vec)
z=0.4
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY14=NY_WSM.solve_all(k_vec)
z=0.5
k=[[0,z],[0.5,z],[1.0,z]]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,101, report=False)
EkfinY15=NY_WSM.solve_all(k_vec)
Show code cell source
fig=plt.figure(figsize=(15,8))
ax=fig.add_subplot(projection="3d")
# make the panes transparent
ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
# make the grid lines transparent
ax.xaxis._axinfo["grid"]['color'] = (1,1,1,0)
ax.yaxis._axinfo["grid"]['color'] = (1,1,1,0)
ax.zaxis._axinfo["grid"]['color'] = (1,1,1,0)
x=k_dist
y=k_dist
y1=zeros(len(k_dist))
y2=zeros(len(k_dist))+0.25
x2=k_dist*10-2.5
X, Y=meshgrid(x,y)
for n in range(len(EkfinY10)):
ax.plot(x,y1, EkfinY10[n,:], c="black", alpha=0.5,linewidth=0.4)
ax.plot(x,y1+0.1, EkfinY11[n,:], c="black", alpha=0.3, linewidth=0.4)
ax.plot(x,y1+0.2, EkfinY12[n,:], c="black", alpha=0.3, linewidth=0.4)
ax.plot(x,y1+0.3, EkfinY13[n,:], c="black", alpha=0.3, linewidth=0.4)
ax.plot(x,y1+0.4, EkfinY14[n,:], c="black", alpha=0.3, linewidth=0.4)
ax.plot(x,y1+0.5, EkfinY15[n,:], c="black", alpha=0.3, linewidth=0.4)
# ax.plot(y1+1,x, EkfinY2[n,:], c="red", alpha=0.5)
# ax.plot(x,EkfinZ[n,:],y1, c="black", alpha=0.5)
ax.set_xlabel("$K_x$")
ax.set_ylabel("$K_z$")
ax.set_zlabel("E[t]")
ax.set_yticks([])
ax.set_zticks([-8,-5,-3,0,5,10, 13])
plt.tight_layout()
ax.view_init(0, -90)
savefig("Planes_Z_TII.pdf")
Como se puede denotar en la figura anterior, la variación de \(k_z\) sila como evolucuiona la relacion de dispersion a lo alrgo de la primera mitad de la zona de Brillouin.
Exploración de la estructura de bandas en el material finito en Z#
Show code cell source
z=0
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ10=NZ_WSM.solve_all(k_vec)
z=0.1
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ11=NZ_WSM.solve_all(k_vec)
z=0.2
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ12=NZ_WSM.solve_all(k_vec)
z=0.3
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ13=NZ_WSM.solve_all(k_vec)
z=0.4
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ14=NZ_WSM.solve_all(k_vec)
z=0.5
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ15=NZ_WSM.solve_all(k_vec)
Show code cell source
fig,ax=plt.subplots(ncols=3,nrows=2,figsize=(20,12),
gridspec_kw = {'wspace':0.2, 'hspace':0.4, 'width_ratios': [1,1,1]})
for n in range(0, len(EkfinX10)):
ax[0,0].plot(k_dist,EkfinZ10[n,:], c='black', alpha=0.6) #la long de Ek fin tiene todo
ax[0,1].plot(k_dist,EkfinZ11[n,:], c='black', alpha=0.6)
ax[0,2].plot(k_dist,EkfinZ12[n,:], c='black', alpha=0.6)#la long de Ek fin tiene todo
ax[1,0].plot(k_dist,EkfinZ13[n,:], c='black', alpha=0.6)
ax[1,1].plot(k_dist,EkfinZ14[n,:], c='black', alpha=0.6)
ax[1,2].plot(k_dist,EkfinZ15[n,:], c='black', alpha=0.6)
for i in range(0,2):
for j in range(0,3):
ax[i,j].spines['right'].set_visible(False)
ax[i,j].spines['top'].set_visible(False)
ax[0,0].set_ylabel(r"$E[t]$",fontsize=26)
ax[1,0].set_ylabel(r"$E[t]$",fontsize=26)
ax[0,0].set_xlabel(r"Finite systemy in $Z|_{k_z=0.0}$",fontsize=26)
ax[0,1].set_xlabel(r"Finite system in $Z|_{k_x=0.1}$",fontsize=26)
ax[0,2].set_xlabel(r"Finite systemy in $Z|_{k_z=0.2}$",fontsize=26)
ax[1,0].set_xlabel(r"Finite system in $Z|_{k_x=0.3}$",fontsize=26)
ax[1,1].set_xlabel(r"Finite systemy in $Z|_{k_z=0.4}$",fontsize=26)
ax[1,2].set_xlabel(r"Finite system in $Z|_{k_x=0.5}$",fontsize=26)
Text(0.5, 0, 'Finite system in $Z|_{k_x=0.5}$')

Show code cell source
z=0
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ10=NZ_WSM.solve_all(k_vec)
z=0.1
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ11=NZ_WSM.solve_all(k_vec)
z=0.2
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ12=NZ_WSM.solve_all(k_vec)
z=0.3
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ13=NZ_WSM.solve_all(k_vec)
z=0.4
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ14=NZ_WSM.solve_all(k_vec)
z=0.5
k=[[z,0],[z,0.5],[z,1.0]]
(k_vec,k_dist,k_node)=NZ_WSM.k_path(k,101, report=False)
EkfinZ15=NZ_WSM.solve_all(k_vec)
Show code cell source
fig=plt.figure(figsize=(15,8))
ax=fig.add_subplot(projection="3d")
# make the panes transparent
ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
# make the grid lines transparent
ax.xaxis._axinfo["grid"]['color'] = (1,1,1,0)
ax.yaxis._axinfo["grid"]['color'] = (1,1,1,0)
ax.zaxis._axinfo["grid"]['color'] = (1,1,1,0)
x=k_dist
y=k_dist
y1=zeros(len(k_dist))
y2=zeros(len(k_dist))+0.25
x2=k_dist*10-2.5
X, Y=meshgrid(x,y)
for n in range(len(EkfinZ10)):
ax.plot(x,y1, EkfinZ10[n,:], c="black", alpha=0.6,linewidth=0.4)
ax.plot(x,y1+0.1, EkfinZ11[n,:], c="black", alpha=0.2, linewidth=0.4)
ax.plot(x,y1+0.2, EkfinZ12[n,:], c="black", alpha=0.3, linewidth=0.4)
ax.plot(x,y1+0.3, EkfinZ13[n,:], c="black", alpha=0.3, linewidth=0.4)
ax.plot(x,y1+0.4, EkfinZ14[n,:], c="black", alpha=0.3, linewidth=0.4)
ax.plot(x,y1+0.5, EkfinZ15[n,:], c="black", alpha=0.3, linewidth=0.4)
# ax.plot(y1+1,x, EkfinY2[n,:], c="red", alpha=0.5)
# ax.plot(x,EkfinZ[n,:],y1, c="black", alpha=0.5)
ax.set_xlabel("$K_x$")
ax.set_ylabel("$K_z$")
ax.set_zlabel("E[t]")
ax.set_yticks([])
ax.set_zticks([-8,-5,-3,0,5,10, 13])
plt.tight_layout()
ax.view_init(0, -90)
savefig("Planes_X_TI.pdf")
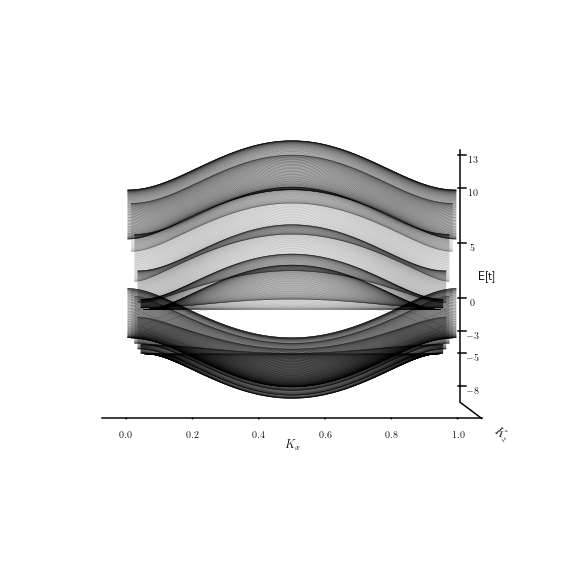
Density of States fo WSM-TI- Histogram#
Una herramienta util para explorar las propiedadfes electroncias de un material es la densidad de estados (DOS). Dicha heramienta nos permitira elucidar la cantidad de estados que hay en los arcos de Fermi en proporción con los que hay en el bulto del material.
For a infinite system#
Show code cell source
# calculate density of states
# first solve the model on a mesh and return all energies
PR = 101
kx,ky,kz = linspace(0,1,PR),linspace(0,1,PR),linspace(0,1,PR)
KX,KY,KZ = meshgrid(kx,ky,kz)
KX,KY,KZ = KX.flatten(),KY.flatten(),KZ.flatten()
K = column_stack((KX,KY,KZ))
# solve the model on this mesh
Edos=WSH.solve_all(K)
# flatten completely the matrixk_dist
Edos=Edos.flatten()
For a finite system#
Show code cell source
L = 100 #Numero de celdas
N_WSM = WSH.cut_piece(L,1,glue_edgs=False) #numero de reps, en la direccion 0x,1y,2z, mi sistema se redujo dimensionalmente
#modo rebanada de jamón
Show code cell source
# calculate density of states
# first solve the model on a mesh and return all energies
PR = 101
kx,ky = linspace(0,1,PR),linspace(0,1,PR)
KX,KY = meshgrid(kx,ky)
KX,KY = KX.flatten(),KY.flatten()
Kf = column_stack((KX,KY))
# solve the model on this mesh
Ekf=N_WSM.solve_all(Kf)
# flatten completely the matrix
Ekf=Ekf.flatten()
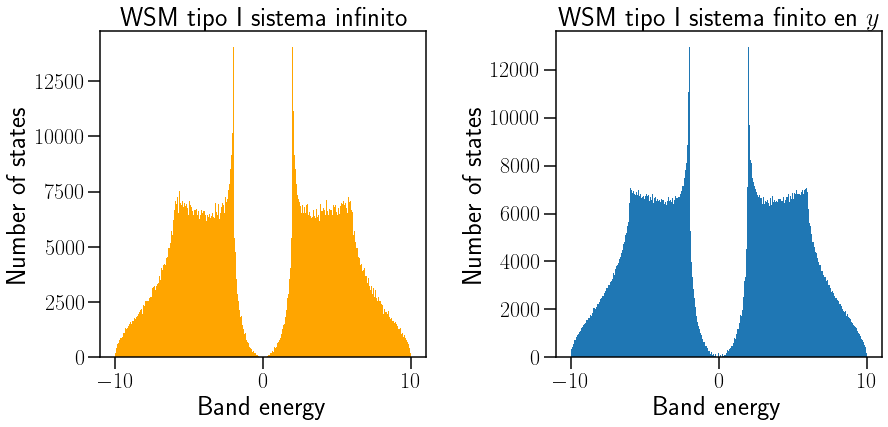
Comparing DOS for a finite system vs a infinite system#
Show code cell source
# plotting DOS
print('Plotting DOS...')
# now plot density of states
fig, ax = plt.subplots(1,2,figsize=(14, 6),
gridspec_kw = {'wspace':0.4, 'hspace':0, 'width_ratios': [1, 1]})
ax[0].hist(Edos,501, color="orange")
ax[0].set_title("WSM tipo I sistema infinito")
ax[0].set_xlabel("Band energy")
ax[0].set_ylabel("Number of states")
ax[1].hist(Ekf,501)
ax[1].set_title("WSM tipo I sistema finito en $y$")
ax[1].set_xlabel("Band energy")
ax[1].set_ylabel("Number of states")
# make an PDF figure of a plot
%time
Plotting DOS...
CPU times: user 2 µs, sys: 0 ns, total: 2 µs
Wall time: 4.53 µs
Show code cell source
fig, ax = plt.subplots(1,2,figsize=(14, 6),
gridspec_kw = {'wspace':0.4, 'hspace':0, 'width_ratios': [1, 1]})
ax[0].hist(Edos,501,label="Sistema infinito")
ax[0].hist(Ekf,501,label="Sistema finito")
ax[0].legend(loc=0,fontsize=14)
ax[0].set_xlabel("Band energy")
ax[0].set_ylabel("Number of states")
ax[1].hist(Ekf,501)
ax[1].hist(Edos,501)
ax[1].set_xlabel("Band energy")
ax[1].set_ylabel("Number of states")
ax[1].set_ylim([0,1000])
ax[1].set_xlim([-0.9,0.9])
savefig("DOS-Fin-vs-DOS-Inf.pdf")
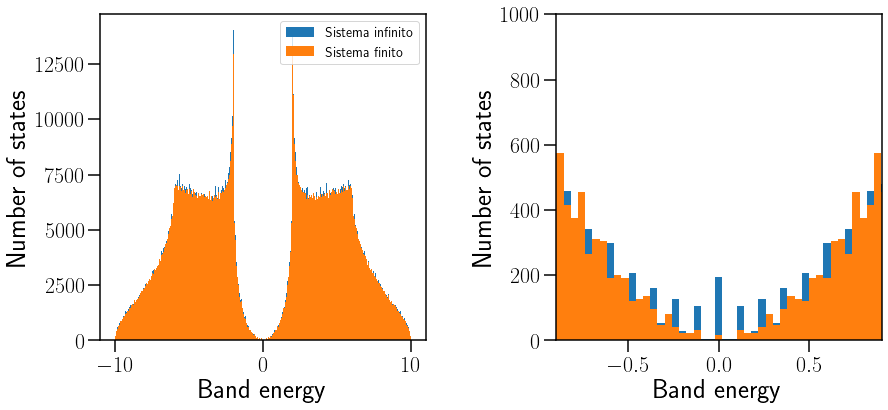
Se puede denotar cómo los arcos de Fermi sólo aparecen cuando el sistema tiene bordes, es decir, cuando se rompe la simetría de traslación.
Densidad de estados usando Funciones de Green.#
La función de Green es uan herramienta matematica que nos permite obtener la DOS de un hamiltoniano independiente del tiempo. A diferencia de los histogramas, tiene la ventaja de que genera curvas suaves.
Show code cell source
Et=linspace(-10,13,1001)
def G(Edos):
GreenP = []
f = 0.01 #al aumentarlo, mejora la fidelidad al hsitograma
for i in Et:
g = sum(1/(i+f*1J-Edos))
GreenP.append(g)
GreenM = []
for i in Et:
g = sum(1/(i-f*1J-Edos))
GreenM.append(g)
N = 2*pi*PR**3
GIP = -imag(GreenP)/N
GRP = real(GreenP)/N
# GIM = imag(GreenM)/N
# GRM = real(GreenM)/N
return GIP, GRP
Show code cell source
G_f,G_inf=G(Edos),G(Ekf)
Show code cell source
# plotting DOS
print('Plotting DOS...')
# now plot density of states ax.legend(loc=0,fontsize=14)
fig, ax = plt.subplots(1,2,figsize=(14, 6) )
ax[0].plot(Et,G_inf[0],label="Sistema finito")
ax[0].plot(Et,G_f[0],label="Sistema infinito")
ax[0].set_xlabel("Band energy")
ax[0].set_ylabel("Number of states")
ax[1].plot(Et,G_inf[0])
ax[1].plot(Et,G_f[0])
ax[1].set_xlim([-1,1])
ax[1].set_ylim([0,0.05])
ax[0].legend(loc=0,fontsize=14)
ax[1].set_xlabel("Band energy")
ax[1].set_ylabel("Number of states")
ax[1].spines['right'].set_visible(False)
ax[1].spines['top'].set_visible(False)
ax[0].spines['right'].set_visible(False)
ax[0].spines['top'].set_visible(False)
#A.u. cuando está normalizada
#Estados por unidad de área y u de energía
# savefig("Green_fuc_DOS")
Plotting DOS...
CPU times: user 2 µs, sys: 0 ns, total: 2 µs
Wall time: 4.53 µs
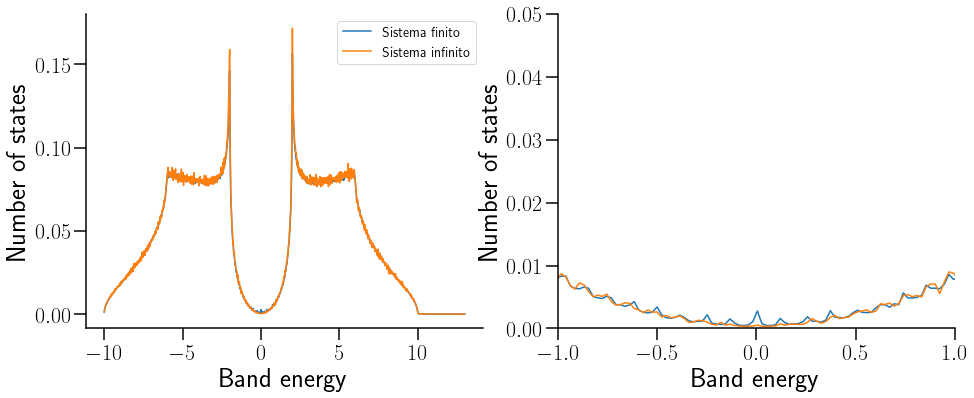
Se puede denotar cómo los arcos de Fermi sólo aparecen cuando el sistema tiene bordes, es decir, cuando se rompe la simetría de traslación.
Densidad de esatdos acomplada con la estructura de bandas#
Show code cell source
fig,ax = plt.subplots(ncols=2,nrows=1,figsize=(14.0,6),
gridspec_kw = {'wspace':0.2, 'hspace':0, 'width_ratios': [ 1,1]})
x=linspace(0,1,101)
for n in range(len(EkfinY10)):
ax[0].plot(x ,EkfinY10[n,:], c="black", alpha=0.5,linewidth=0.4)
ax[0].plot(x ,EkfinY11[n,:], c="black", alpha=0.3, linewidth=0.4)
ax[0].plot(x,EkfinY12[n,:], c="black", alpha=0.3, linewidth=0.4)
ax[0].plot(x, EkfinY13[n,:], c="black", alpha=0.3, linewidth=0.4)
ax[0].plot(x, EkfinY14[n,:], c="black", alpha=0.3, linewidth=0.4)
ax[0].plot(x, EkfinY15[n,:], c="black", alpha=0.3, linewidth=0.4)
#la long de Ek fin tiene todo
ax[0].set_xticks(k_node) # puntos de alta simetria, valor que correspomde en k_path
ax[0].set_xticklabels(k_label )
for i in range(0,2):
ax[i].set_ylim(-11,13)
# xsticklabels(k_label)
ax[i].spines['right'].set_visible(False)
ax[i].spines['top'].set_visible(False)
ax[0].set_ylabel(r"$E[t]$",fontsize=26)
ax[0].set_xlabel(r"$K_x$",fontsize=26)
ax[1].plot(G_inf[0],Et)
savefig("Dispersion-DOS_TII.pdf",bbox_inches="tight")
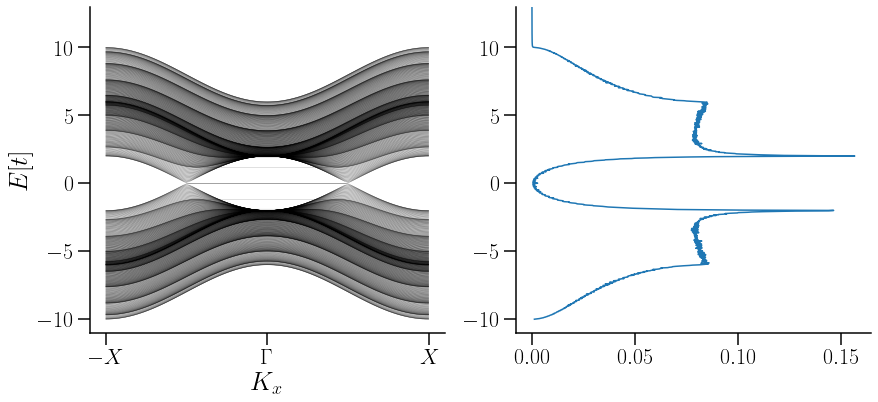
En la figura anterior se puede notar cómo los arcos de Fermi aparecen en una \(E[t]=0\).
Show code cell source
trapz(G_f[0], Et)
0.9991432821048173
La celda anterior comprueba que la densidad de estados dada por la función de Green está normalizada.
IPR#
El IPR o Inverse Participation Ratio (IPR, por sus siglas en inglés) es una cantidad que perimte saber qué tan lo laizados están los estados electronicos en un material. En esta sección se presenta un grafico coloreado con el Log|IPR|, de manera que los colores más obsucuros elucidarán qué estados son los más localizados.
Show code cell source
print("building finite sistems")
L=100
NY_WSM=WSH.cut_piece(L,1,glue_edgs=False) #numero de reps, en la direccion 0x,1y,2z, mi sistema se redujo dimensionalmente
#modo rebanada de jamón
# NNYZ_WSM=NY_WSM.cut_piece(L,2,glue_edgs=False)
# NNYX_WSM=NY_WSM.cut_piece(L,0,glue_edgs=False)
building finite sistems
Show code cell source
print("Extracting eigenvectors and eigenvalues")
a=1
k = [[0,0],[a/2,0],[a,0]] #unidades en unidades de V de red 1=2pi/a
k_label1=[r"$\Gamma$","X",r"$\Gamma$"]
(k_vec,k_dist,k_node)=NY_WSM.k_path(k,501, report=False)
Ekfin2YZ, ψk1=NY_WSM.solve_all(k_vec,eig_vectors=True)
# savez_compressed("Data_YZ_γ={}".format(γ), Dk=k_dist,DEk=Ekfin2YZ, U=ψk1)
# k = [[0],[a/2],[a]] #unidades en unidades de V de red 1=2pi/a
# k_label2=[r"$\Gamma$","Z",r"$\Gamma$"]
# (k_vec,k_dist,k_node)=NNYX_WSM.k_path(k,101, report=False)
# Ekfin2YX, ψk2=NNYX_WSM.solve_all(k_vec,eig_vectors=True)
# savez_compressed("Data_YX_γ={}".format(γ), D_k=k_dist,D_Ek=Ekfin2YX, U=ψk2)
Extracting eigenvectors and eigenvalues
Show code cell source
print("Calculating IPR")
nBands,nkpts,nsites= shape(ψk1)
Ik1 = []
index = []
for i in range(nBands):
In = []
for j in range(nkpts):
eigvec=ψk1[i,j]
suma4= vdot(eigvec*eigvec, eigvec*eigvec)
suma2= vdot(eigvec,eigvec)
In.append(real(suma4/suma2))
Ik1.append(In)
Ik1 = array(Ik1)
savez_compressed("Data_Ik1_γ={}".format(γ),D_Ik1=Ik1)
Calculating IPR
Show code cell source
fig,ax = plt.subplots(ncols = 1,nrows = 1, figsize = (6,6)) #
for n in range(len(Ekfin2YZ)):
Ekval=Ekfin2YZ[n,:]
amp =Ik1[n,:]
cmap = ax.scatter(k_dist,Ekval,c =log10(amp), cmap = 'cubehelix_r',s = 0.5, alpha=0.5,vmax=0, vmin=-3,rasterized=True)
ax.set_xticks(k_node) # puntos de alta simetria, valor que correspomde en k_path
ax.set_xticklabels(k_label)
ax.set_xlabel(r"$K_X$")
ax.set_ylabel("E")
# ax.set_ylim(-2,2)
fig.colorbar(cmap)
savefig("IPR_Y_γ={}.pdf".format(γ),bbox_inches="tight")

Interactivo#
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
Show code cell source
#Parámetros
@interact(a=(0,1,0.1),m=(0,1.5,0.1), tx=(0,1.5,0.1),t=(0,1.5,0.1),γ=(0,1.5,0.1))
def WSHTot(a=1.0,m=1.0,tx=0.5, t=0.5, γ=1.5):
#hopping perpendicular
k_0= pi/2
##################----------------Inicia TB--------------------#######################
lat = [[a,0,0],[0,a,0],[0,0,a]]
orb = [[0,0,0],[1/2,1/2,1/2]] #H, solo los sitios A[000] B1/2[111]
WSH = tb_model(3,3,lat,orb)
#DIAGONAL
#γ*(cos(k_x)-cos(k_0))-2*t*sin(k_z)
# γ[coskx]
WSH.set_hop(γ/2, 0, 0,[1,0,0])#de que sitio a que sitio va el hoping, [la exp que lleva ese parametro], Conjugado ya no es
# -2tsinkz #necesario, está implícito porque es Hermitiano.
WSH.set_hop(-t/1J, 0, 0,[0,0,1])
#Hermitiano [1,1]
WSH.set_hop(γ/2, 1, 1,[1,0,0])
WSH.set_hop(t/1J, 1, 1,[0,0,1])
WSH.set_onsite([-γ*cos(k_0),-γ*cos(k_0)]) # No hay hooping, es energia
#FUERA DE LA DIAGONAL
# -[m*(2-cos(k_y)-cos(k_z))+2*tx*(cos(k_x)-cos(k_0))]+2J*t*sin(k_y)
# 2txcosk_0
WSH.set_hop(-2*m+2*tx*cos(k_0), 0, 1,[0,0,0])
#mcosky+ 2itsin(ky)
WSH.set_hop(m/2+t, 0, 1,[0,1,0])
WSH.set_hop(m/2-t, 0, 1,[0,-1,0])
# mcoskz
WSH.set_hop(m/2, 0, 1,[0,0,1])
WSH.set_hop(m/2, 0, 1,[0,0,-1])
# tx(coskx)
WSH.set_hop(-tx, 0, 1,[1,0,0])
WSH.set_hop(-tx, 0, 1,[-1,0,0])
###############---------Inicia extraccion de información-----------##############
k = [[-0.5,0,0],[0,0,0.0],[0.5,0,0]] # Punto por los cuales que quiero que pase. Son los punto de al simetria
#unidades en unidades de V de red 1=2pi/a
k_label = ["-Z",r"$\Gamma$","Z"]
(k_vec,k_dist,k_node) = WSH.k_path(k,1001,report=False)
Ek,U = WSH.solve_all(k_vec,eig_vectors=True)
#######################---Graficos----######################
pm=plot(k_dist,Ek[0,:])
pd=plot(k_dist,Ek[1,:])
xticks(k_node,labels=k_label) # puntos de alta simetria, valor que correspomde en k_path
# xsticklabels(k_label)
xlabel(r"$K_Z$")
ylabel("E")
Subplots#
Show code cell source
def WSHTot(a=1.0,m=1.0,tx=0.5, t=0.5, γ=1.5):
#hopping perpendicular
k_0= pi/2
##################----------------Inicia TB--------------------#######################
lat = [[a,0,0],[0,a,0],[0,0,a]]
orb = [[0,0,0],[1/2,1/2,1/2]] #H, solo los sitios A[000] B1/2[111]
WSH = tb_model(3,3,lat,orb)
#DIAGONAL
#γ*(cos(k_x)-cos(k_0))-2*t*sin(k_z)
# γ[coskx]
WSH.set_hop(γ/2, 0, 0,[1,0,0])#de que sitio a que sitio va el hoping, [la exp que lleva ese parametro], Conjugado ya no es
# -2tsinkz #necesario, está implícito porque es Hermitiano.
WSH.set_hop(-t/1J, 0, 0,[0,0,1])
#Hermitiano [1,1]
WSH.set_hop(γ/2, 1, 1,[1,0,0])
WSH.set_hop(t/1J, 1, 1,[0,0,1])
WSH.set_onsite([-γ*cos(k_0),-γ*cos(k_0)]) # No hay hooping, es energia
#FUERA DE LA DIAGONAL
# -[m*(2-cos(k_y)-cos(k_z))+2*tx*(cos(k_x)-cos(k_0))]+2J*t*sin(k_y)
# 2txcosk_0
WSH.set_hop(-2*m+2*tx*cos(k_0), 0, 1,[0,0,0])
#mcosky+ 2itsin(ky)
WSH.set_hop(m/2+t, 0, 1,[0,1,0])
WSH.set_hop(m/2-t, 0, 1,[0,-1,0])
# mcoskz
WSH.set_hop(m/2, 0, 1,[0,0,1])
WSH.set_hop(m/2, 0, 1,[0,0,-1])
# tx(coskx)
WSH.set_hop(-tx, 0, 1,[1,0,0])
WSH.set_hop(-tx, 0, 1,[-1,0,0])
###############---------Inicia extraccion de información-----------##############
k = [[-0.5,0,0],[0,0,0.0],[0.5,0,0]] # Punto por los cuales que quiero que pase. Son los punto de al simetria
#unidades en unidades de V de red 1=2pi/a
k_label = ["-X",r"$\Gamma$","X"]
(k_vec,k_dist,k_node) = WSH.k_path(k,1001,report=False)
Ek,U = WSH.solve_all(k_vec,eig_vectors=True)
return (k_dist, Ek, U, k_node, k_label )
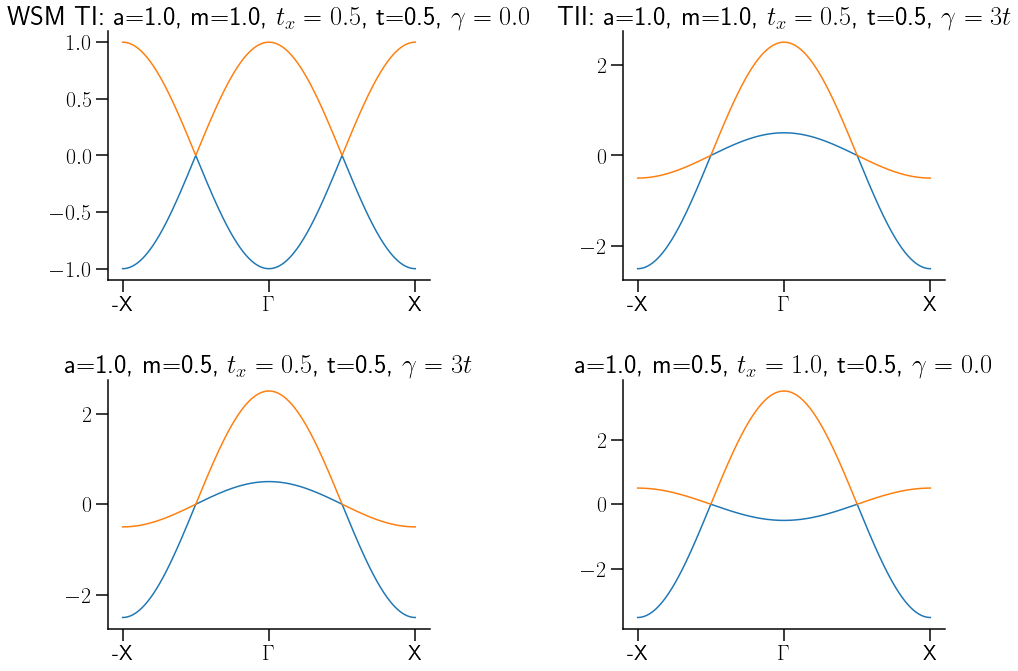
Show code cell source
fig, axs = plt.subplots(2, 2,figsize=(15, 11),
gridspec_kw = {'wspace':0.6, 'hspace':0.4, 'width_ratios': [1, 1]})
k_dist, Ek, U, k_node, k_label=WSHTot(a=1.0,m=1.0,tx=0.5, t=0.5, γ=0)
axs[0, 0].plot(k_dist,Ek[0])
axs[0, 0].plot(k_dist, Ek[1])
axs[0, 0].set_xticks(k_node)
axs[0, 0].set_xticklabels(k_label)
axs[0, 0].set_title("WSM TI: a=1.0, m=1.0, $t_x=0.5$, t=0.5, $\gamma=0.0$")
k_dist, Ek, U, k_node, k_label=WSHTot(a=1.0,m=1-0,tx=0.5, t=3.5, γ=1.5)
axs[0, 1].plot(k_dist, Ek[0])
axs[0, 1].plot(k_dist, Ek[1])
axs[0, 1].set_xticks(k_node)
axs[0, 1].set_xticklabels(k_label)
axs[0, 1].set_title("TII: a=1.0, m=1.0, $t_x=0.5$, t=0.5, $\gamma=3t$")
k_dist, Ek, U, k_node, k_label=WSHTot(a=1.0,m=0.5,tx=0.5, t=3.0, γ=1.5)
axs[1, 0].plot(k_dist, Ek[0])
axs[1, 0].plot(k_dist, Ek[1])
axs[1, 0].set_xticks(k_node)
axs[1, 0].set_xticklabels(k_label)
axs[1, 0].set_title("a=1.0, m=0.5, $t_x=0.5$, t=0.5, $\gamma=3t$")
k_dist, Ek, U, k_node, k_label=WSHTot(a=1.0,m=0.5,tx=1.0, t=0.5, γ=1.5)
axs[1, 1].plot(k_dist, Ek[0])
axs[1, 1].plot(k_dist, Ek[1])
axs[1, 1].set_xticks(k_node)
axs[1, 1].set_xticklabels(k_label)
axs[1, 1].set_title("a=1.0, m=0.5, $t_x=1.0$, t=0.5, $\gamma=0.0$")
for ax in axs.flat:
# ax.set_xlim(0,2)
# ax.set_ylim(-4,)
#
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# puntos de alta simetria, valor que correspomde en k_path
savefig("VarMinModls.pdf",bbox_inches='tight')